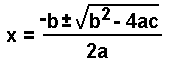
STEP 1: Identify the major species in solution:

$HC$₃H₅O₃ ( weak acid )

$C$₃H₅O₃^- ( conjugate base of $HC$₃H₅O₃ )

$Na+$ ( spectator ion )

$H$₂O ( very weak acid or base )

STEP 2: Determine the equilibrium reaction involved:

$HC$₃H₅O₃ and $C$₃H₅O₃^- will react together to affect the pH of the solution:

$HC$₃H₅O₃ (aq) H⁺ (aq) + C₃H₅O₃^- (aq)

STEP 3: Create an I.C.E. grid:

STEP 4: Substitute equilibrium concentrations into the equilibriuum constant expression, then simplify and solve the expression:

Because $K$_a x 1000 is larger than both 0.10 and 0.12, simplification is not possible. Thus, to reach the solution, it is necessary to use the quadratic formula to solve. Rearrangement gives:

Using the quadratic formula:

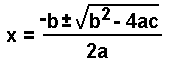
Because we cannot have a negative concentration of $H+$ ions,

STEP 5: Calculate the pH:

pH = - log$[H+]$ = - log( 1.7 x $10-4$ ) = 3.77

How much HCl must be added to 1.00 L of 0.10 M sodium lactate ( $NaC$₃H₅O₃ ) to make a buffer of the same pH as found in the previous example (3.77)?

STEP 1: Calculate the equilibrium concentration of $H+$ that will produce the given pH:

$[H+]\; =\; 10-pH$

$[H+]\; =\; 10-3.77=\; 1.7$ x $10-4$

STEP 2: Determine the equilibrium which must take place for this solution to be a buffer:

For a buffer effect to take place, the solution must contain both the weak acid $HC$₃H₅O₃ and its conjugate base. The equilibrium reaction is therefore:

$HC$₃H₅O₃ (aq) H⁺ (aq) + C₃H₅O₃^- (aq)

STEP 3: Create an I.C.E. grid:

This time we will call $x$ the initial concentration of $H+$. Because we know that the equilibrium $[H+]$ is so small, we can assume that nearly all the initial $H+$ is used up.

$HC$₃H₅O₃ (aq) H⁺ (aq) + C₃H₅O₃^- (aq)

STEP 4: Substitute the equilibrium concentrations into the equilibrium constant expression:

STEP 5: Solve for $x$:

STEP 6: Convert this answer to moles of HCl:

How much NaOH must be added to 1.00 L of 0.10 M lactic acid, $HC$₃H₅O₃ to make a buffer of the same pH as the first example (3.77) ?

STEP 1 : Calculate the equilibrium concentration of $OH-$ that will produce the given pH

$[H+]\; =\; 10-pH=\; 10-3.77=\; 1.7$ x $10-4M$

$[OH-]\; =\; \{\; K$_W / [H⁺] } = { 1.0 x $10-14/\; 1.7$ x $10-4M\; \}\; =\; 5.9$ x $10-11M$

STEP 2 : Determine the equilibrium which must take place for this solution to be a buffer:

Once again, the weak acid and the conjugate base must be present. This time, however, we want $OH-$ in the equation.

$HC$₃H₅O₃ (aq) + OH^- (aq) H₂O (l) + C₃H₅O₃^- (aq)

STEP 3: Create an I.C.E. grid

This time we will call $x$ the inital concentration of $OH-$. The given equilibrium should proceed almost to completion, so we will assume nearly all the $OH-$ is used up. Its equilibrium $[OH-]$ is so small :

$HC$₃H₅O₃ (aq) + OH^- (aq) H₂O (l) + C₃H₅O₃^- (aq)

STEP 4: Substitute the equilibrium concentrations into the equilibrium constant expression:

This equilibrium is the reverse reaction for a base reacting with water. Therefore, the K we must use is $\{1\; /\; K$_b}.

STEP 5: Solve for $x$:

STEP 6: Convert this answer to moles of NaOH: