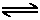 H+ + A-
H+ + A-H2O
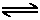 H+ + OH-
H+ + OH-Until now, we have assumed that the pH of an aqueous solution of acid or base is determined only by the dissociation of the acid or base itself. However, as described in earlier sections, there is always another acid or base present in the solution- water. Since water dissociates to form H+ and OH-, it affects the pH of the solution. Usually we ignore this effect because water is only very weakly acidic and basic, allowing us to assume that its contribution to the pH of the solution is negligible compared to that of other acids or bases present. However, this assumption is not valid when the concentrations of H+ or OH- due to the dissociation of water are comparable to those due to the dissociation of other acids or bases in solution.
Here we consider the case where water produces a [H+] comparable to that produced by an acid in solution. However, an exactly equivalent case exists for the [OH-] and bases.
At 25oC, pure water dissociates to give a [H+] of 1.0x10-7M. Thus, whenever the [H+] due to the acid in solution is low enough to be close to 1.0x10-7M, the dissociation of water will significantly affect the pH of the solution. This means that we must discard the assumption that water makes a negligible contribution to the pH in order to accurately calculate the pH of the solution. (We will see later how to tell whether or not the [H+] is low enough for water to contribute to the pH.)
Consider a dilute acid solution. The pH will be determined by following two equilibria:
HA 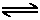 H+ + A-
H+ + A-
H2O 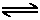 H+ + OH-
H+ + OH-
We can easily predict what would happen if each of these equilibria was the only source of of H+ in the solution:
Because both HA and H2O are present, the actual [H+] will be greater than either [H+]a or [H+]w. However, it will be less than the sum [H+]a+[H+]w. This is because each of the two equilibria will be shifted to the left by the presence of H+ from the other reaction, causing each to produce less H+ than if it were the only equilibrium present.
The details of the calculation are different for strong and weak acids. Let's look first at the strong acid case.
| Learning Goal 30 |
|---|
| Calculate the pH of a strong acid solution, taking the dissociation of water into consideration. |
This is actually quite a simple calculation.
The pH of the solution is controlled by two reactions:
HA  H+ + A-
H+ + A-
H2O 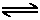 H+ + OH-
H+ + OH-
Since HCl is a strong acid, it dissociates completely, with no equilibrium to adjust to the presence of additional H+ ions. Thus, we can consider HCl to dissociate first, with H2O then responding by dissociating according to Kw without affecting the dissociation of the HCl.
Here, the two reactions controlling the pH of the solution are:
HCl  H+ + Cl-
H+ + Cl-
H2O 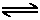 H+ + OH-
H+ + OH-
We consider HCl to dissociate first, with H2O then responding.
Since the concentration of acid is 2.0x10-7 M, HCl will produce a [H+] of 2.0x10-7. Using this as the initial [H+] in the equilibrium dissociation of water, we can find the equilibrium [H+] with an I.C.E. table:
| INITIAL
| CHANGE
| EQUILIBRIUM
| |
|---|
Kw = [H+]eq*[OH-]eq
1.0x10-14 = (2.0x10-7 + ) * x
1.0x10-14 = x2 + (2.0x10-7 * x)
0 = x2 + (2.0x10-7 * x) - 1.0x10-14
Using the quadratic formula, we get x = 4.14x10-8 M or x = -2.41x10-7 M. Since [OH-] = x and we cannot have a negative [OH-], x = 4.14x10-8 M.
So, [H+]eq = (2.0x10-7 + 4.14x10-8) M = 2.41x10-7 M, giving a pH of 6.62.
Click here to see two alternate methods of performing this calculation.
An analogous situation exists for weak acids in which the [H+] due to acid dissociation is comparable to the [H+] due to water dissociation (1.0x10-7 M). Unlike strong acids, where water dissociation is important only when a very dilute acid is involved, water dissociation can contribute to the pH of a weak acid solution if the acid is very dilute, very weak, or dilute and weak. (Why?)
The actual calculation of the pH of a weak acid solution in which water dissociation is considered is much more complicated than the one for a strong acid solution, and is above the level of this tutorial. For those who are interested, the complete calculation is presented here. However, for this tutorial, students need only know how to determine whether or not water will contribute significantly to the pH of a weak acid solution, which is dealt with below.
| Learning Goal 31 |
|---|
| Determine whether or not water needs to be considered in order to perform an accurate calculation of the pH of a strong acid solution. |
As we have seen, a lot more calculation is needed when we consider the dissociation of water in calculating pH than when we ignore it. So, we want to only do those extra calculations when they will make a significant difference in the answer. How do we know whether or not water will contribute significantly to the pH?
For strong acids, we can figure this out by rearranging a general equation derived in the second alternate solution to the strong acid example presented above:
Kw = [H+]2 - Ca*[H+]
Ca*[H+] = [H+]2 - Kw
Ca = ( [H+]2 - Kw ) / [H+]
Now, we see that if [H+]2 >> Kw, the equation simplifies to
Ca = ( [H+]2 ) / [H+] = [H+]
Here, [H+] = Ca just like in a strong acid solution in which water is ignored. So, we can ignore the dissociation of water if [H+]2 >> Kw.
For weak acids, we consider an equation derived during the full mathematical treatment of weak acid solutions in which water dissociation is considered:
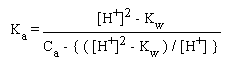
Again, if [H+]2 >> Kw, this equation simplifies to
Ka = [H+]2 / ( Ca - [H+] )
which is the equation resulting from a normal weak acid calculation that ignores the effect of the dissociation of water. So, just like strong acids, we can ignore the dissociation of water if [H+]2 >> Kw.
For both strong and weak acids, we will consider >> to mean "at least 100 times greater":
[H+]2 >> 1.0x10-14
[H+]2 > 100 * 1.0x10-14
[H+]2 > 1.0x10-12
[H+] > 1.0x10-6 M
So we can conclude that if the [H+] produced by the acid without considering the dissociation of water is greater than 1.0x10-6 M, the answer is accurate enough. However, if the [H+] produced by the strong acid is less than 1.0x10-6, we need to redo the calculation taking water into account.


