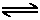 H+ + A-
H+ + A-H2O
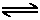 H+ + OH-
H+ + OH-As with the strong acid case, the pH will be determined by the dissociation of the acids HA and water:
HA 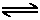 H+ + A-
H+ + A-
H2O 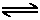 H+ + OH-
H+ + OH-
The difference here is that neither acid dissociates completely, so both equilibria are affected by the H+ produced by the other equilibrium. Thus, neither HA nor water can be considered to dissociate first without later being affected by the response of the other as in the alternate solutions to the strong acid problem. The two equilibria MUST be considered simultaneously.
This time, HA does not dissociate completely, so we cannot eliminate any unknowns. Thus, we have four unknown concentrations at equilibrium: [HA], [A-], [H+] and [OH-]. To solve for all four concentrations, we need four independent equations relating them.
As with the strong acid case, we can use the Kw expression:
(1) Kw = [H+] * [OH-]
We can also use the Ka expression for the weak acid:
(2) Ka = [H+] * [A-] / [HA]
Also as with the strong acid case, we can use the principle of charge balance to generate a third equation:
(3) [A-] + [OH-] = [H+]
The fourth equation comes from the conservation of the chemical species A during the dissociation of HA- All of the HA initially present ends up as either HA or A-:
[total A]initial = [total A]eq
(4) Ca = [HA] + [A-]
Our task now is to combine these equations in such a way as to eliminate all unknowns except for [H+], leaving [H+] defined in terms of the known constants Ca, Ka and Kw.
STEP 1: Eliminate [OH-]
We rearrange equation (1) to solve for [OH-]
[OH-] = Kw / [H+]
and then substitute [OH-] into equation (3), the charge balance equation:
( Kw / [H+] ) + [A-] = [H+]
STEP 2: Eliminate [A-]
We rearrange the substituted charge balance equation to solve for [A-]
[A-] = [H+] - ( Kw / [H+] )
[A-] = ( [H+]2 - Kw ) / [H+]
and then substitute [A-] into equation (4), the equation showing the conservation of A:
Ca = [HA] + { ( [H+]2 - Kw ) / [H+] }
STEP 3: Eliminate [HA]
We rearrange the substituted conservation of A equation to solve for [HA]
[HA] = Ca - { ( [H+]2 - Kw ) / [H+] }
and then substitute [HA], [H+] and [A-] into equation (2), the Ka expression:
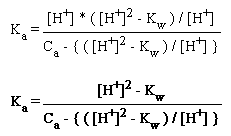
In order to solve this equation, we rearrange it to form a polyomial of [H+]:
[H+]3 + Ka[H+]2 - (KaCa + Kw)[H+] - KaKw = 0
Unfortunately, we do not have a "cubic formula" to solve this equation exactly for [H+], so we will have to solve it approximately. We could just guess at [H+] until we find one that comes very close to solving the equation. However, that could take a lot of time, so we will use a more systematic approach- successive approximation.
To perform successive approximation on this cubic equation, we need to rearrange it into a form where the left side contains only the variable [H+] and the right side also contains at least one [H+] term. Then, we can guess at [H+] and substitute that guess into the right side as if it were a known constant, in order to calculate a better guess for [H+].
Rearranging the cubic equation, we get
[H+]' = { [H+]3 + Ka[H+]2] - KaKw } / {KaCa + Kw }
Note that we have designated the left side as [H+]' in order to make it clear that this is the new guess at [H+] that we are calculating from the old one.
We now proceed by repeatedly guessing at [H+] and improving the guess using this equation. Once [H+]' is close enough to our previous guess at [H+] for our liking, we stop the process and use [H+]' as the [H+] in the weak acid solution, which we can use to calculate the pH.
